Quantitative Data

Describing Data

Other terms that are used to describe data types are summarised here.

Categorical versus Numerical

Data that represent categories, such as dichotomous (two categories) and nominal (more than two categories) observations, are collectively called categorical (qualitative).

Data that can be counted or measured using a numerically defined method are called numerical (quantitative).

Discrete versus Continuous

A discrete value is a value that can only take on specific, distinct, and separate numerical values within a defined range. Examples include the number of members in a team or students in a class.

Continuous data can take any value within a range and has a true zero point.

Variables

Research variables are characteristics that can take on different values, and can be measured, manipulated and analysed.

Types of Variables
Independent Variable (Exposure)	Dependent Variable (Outcome)
A factor that would be associated with the outcome you plan to measure. This can be manipulated or controlled.	The variable you plan to measure to determine whether there was an impact of the exposure on the expected outcome. This is the variable you would expect to change and would attribute the change to the exposure.

Moderating variables have a contingent effect on the relationship between the independent and dependent variables.

Covariates are variables that are related to both the independent and dependent variables.

Exploratory Analysis

Exploratory analysis involves visually observing the data using graphs to understand its distribution.

Many statistical techniques assume that the dependent variable is ‘normally’ distributed (symmetrical, bell-shaped curve with the greatest frequency of scores in the middle and fewer at both ends of the curve).

Therefore, before you decide what statistical technique to employ, you should check the distribution of your variables.

The procedure in SPSS to determine whether a variable is normally distributed is the explore option.

A step-by-step guide on how to run a Kolmogorov-Smirnov test in SPSS can be accessed here.

Kolmogorov-Smirnov test

You will find the results for the Kolmogorov-Smirnov test, in the output section, tests for normality.

P > 0.05 non-significant therefore normally distributed

P < 0.05 significant non-normally distributed

Histogram and Q-Q Plots

Normality can also be assessed by reviewing histogram plots and Q-Q plots, to determine whether the variable is normally distributed or skewed.

If you interpret the variable to be normally distributed you can consider running parametric tests and non-parametric tests for non-normally distributed variables.

Measuring Central Tendency

This involves identifying a single number that represents the center value of a set of data.

Think of it as figuring out the "average" value.

There are three main ways to do this:

Mean: gives you the average
Median: gives you the middle number
Mode: gives you the most common value

These values will change, depending on how the data is distributed.

One of the most useful graphs to help you understand how your data is distributed is a histogram.

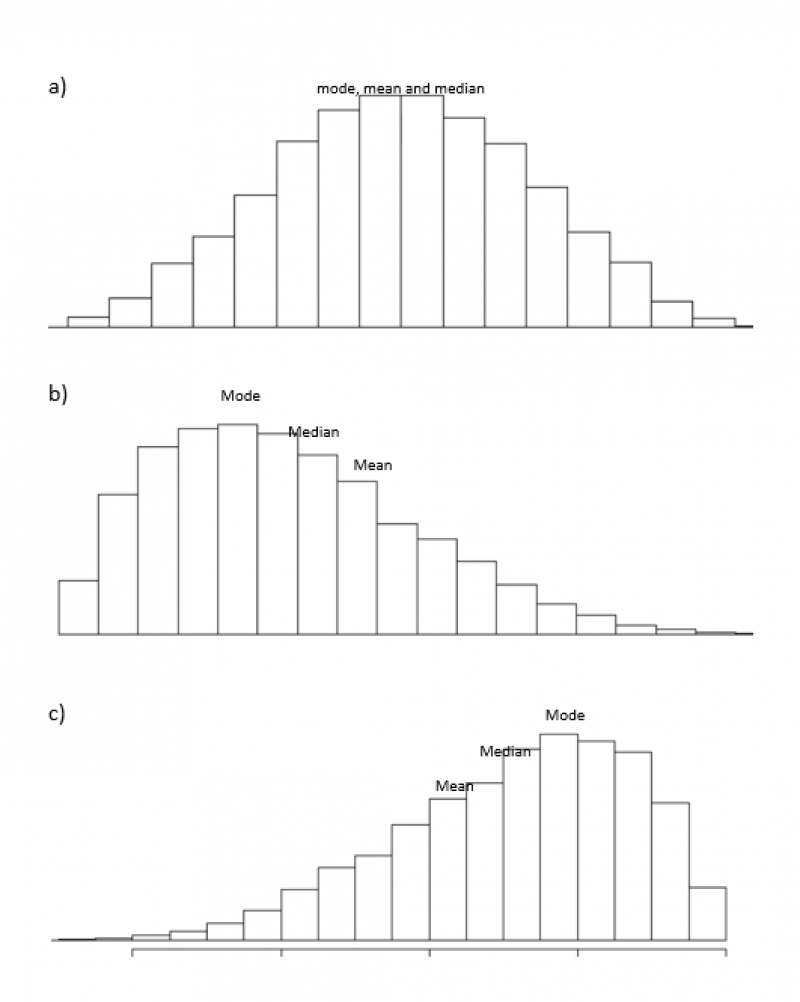
See the picture below to help visualize some of the ways in which data can be distributed.

Data Distributions

a) Symmetrical Distribution

The data is normally distributed and is often referred to as bell-shaped.

The mean, median, and mode are all the same value.

b) Positively Skewed Distribution (Right-Skewed)

The mean is higher than the median, which is higher than the mode.

c) Negatively Skewed Distribution (Left Skewed)

The mean is lower than the median, which is lower than the mode.

Transforming Data

If the normality assumption is not fulfilled, you can try transforming the data to fix the non-normal distributions.

Browse the Library catalogue for books to help you with this, including the SPSS Survival Manual

Univariate Analysis

Univariate analysis is a statistical technique used to analyse one variable at a time. Key aspects of univariate analysis include running descriptive statistics and frequencies.

These are considered preliminary steps in data analysis before exploring relationships between variables.

Descriptive Statistics

Descriptive statistics are crucial because they:

Simplify large amounts of data in a sensible way.
Help identify patterns, trends, and anomalies in the data.
Provide a foundation for further statistical analysis, including inferential statistics.

Running descriptive statistics in SPSS includes exploring the measure of central tendency which we have covered already and also includes measures of variability which we will cover now.

Measures of Variability

These metrics describe the spread of the data.

Range: The difference between the highest (maximum or largest) and lowest (minimum or smallest) values.
Variance: A measure of how much the values in the dataset differ from the mean.
Interquartile Range: This is the difference between the 1st and 3rd quartile. A larger interquartile range means a more dispersed distribution of data.
Standard Deviation: The square root of the variance, providing a measure of spread in the same units as the data. A large standard deviation means the data is very spread out, while a small standard deviation means the data is very close together.

Choosing a Statistical Test

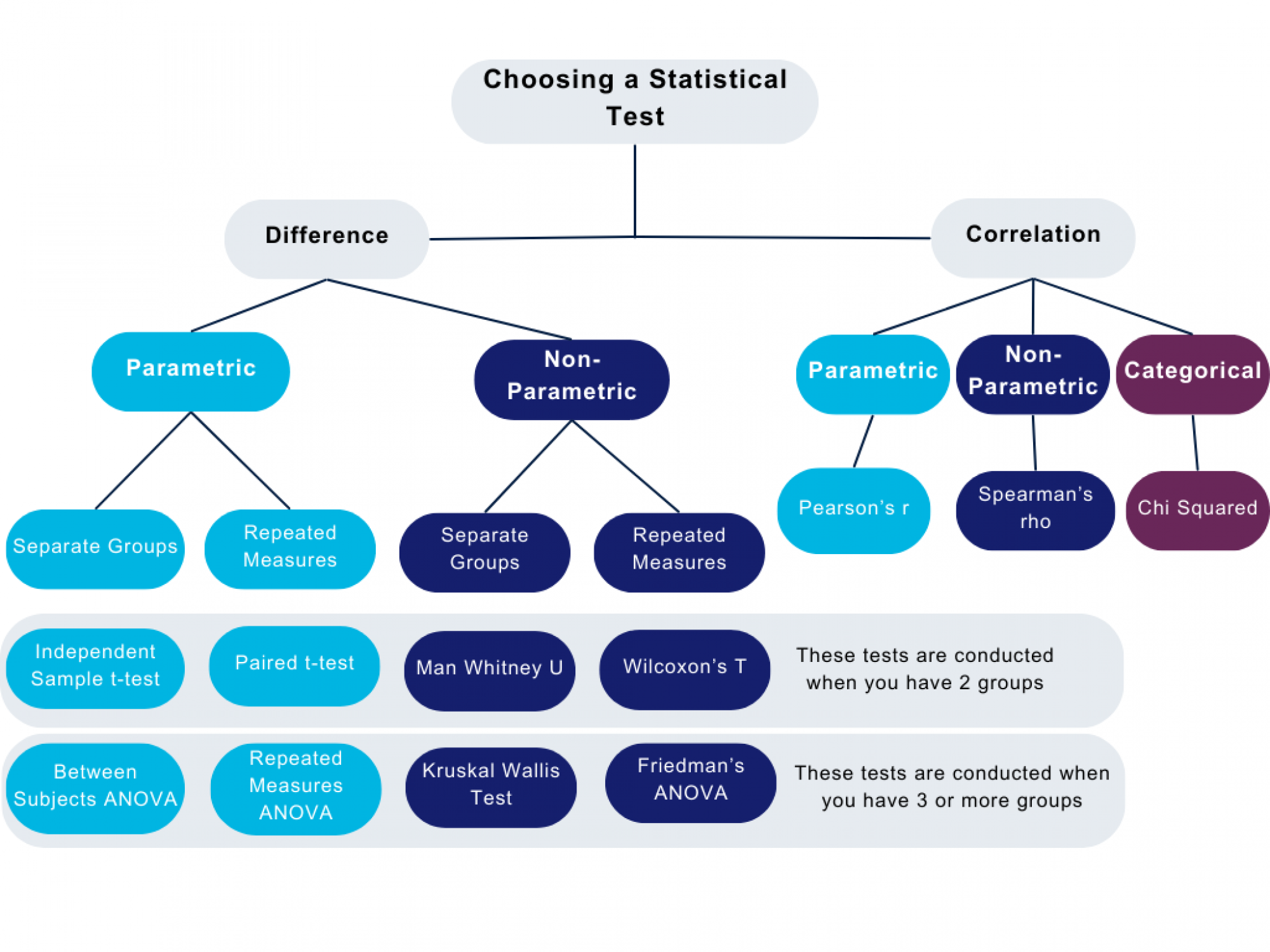
A flow diagram to help students identify the correct statistical test depending on whether the analysis is testing for differences or correlations: Testing for Differences Between Means: Two Groups: Parametric test: Independent sample t-test Non-parametric equivalent: Mann-Whitney U test Three or More Groups: Parametric test: Between-subjects ANOVA Non-parametric equivalent: Kruskal-Wallis test Testing for Differences with Repeated Measures: Two Groups: Parametric test: Paired t-test Non-parametric equivalent: Wilcoxon signed-rank test Three or More Groups: Parametric test: Repeated measures ANOVA Non-parametric equivalent: Friedman’s ANOVA Testing for Correlations: Parametric Data: Test: Pearson’s r Non-parametric Data: Test: Spearman’s rho Categorical Data: Test: Chi-square analysis

The figure above has been designed to give you an indication of types of tests you can run, depending on whether your data is normally distributed or non-normal. These are not all the possible tests you can run but rather a starting point to help you in your decision making.

Parametric Tests

In this section, you will find information about some types of parametric tests used in data analysis.

These tests are powerful tools for making inferences about populations. Whether you are looking to compare means, analyze variances, or test correlations, this guide will provide you with some insights and examples to understand and apply tests such as t-tests, ANOVA, and correlation analysis.

T-Test

T-tests are statistical tests used to determine if there is a significant difference between the means of two groups.

Here we delve into the different types of T-Test you can run.

One sample T-Test	Compares the mean of a single sample to that of a known or hypothesised population mean to determine if there is a difference. It is used to determine if the sample mean is significantly different from a hypothesized value.	1 continuous dependent variable 1 categorical (nominal or ordinal) independent variable	Compare the mean blood pressure of a group of patients on a certain medication, with a predetermined value (normal blood pressure)
Independent two sample T-Test	Compares the mean of one distinct group to the mean of another distinct group to see if they are significantly different from each other. It assumes that the variances of the two groups are equal (homogeneity of variance).	1 continuous dependent variable (performance score) 1 categorical independent variable (gender)	Compare mean performance scores between men and women
Paired Sample T-Test	Compares the means of two related groups. It is used when the same subjects are measured twice (e.g. before and after treatment) or when there is a natural pairing (e.g. twin studies).	1 categorical independent variable (same people pre and post) 1 continuous dependent variable (anxiety score)	Does a meditation course decrease levels of anxiety

One sample T-Test

Compares the mean of a single sample to that of a known or hypothesised population mean to determine if there is a difference.

It is used to determine if the sample mean is significantly different from a hypothesized value.

1 continuous dependent variable

1 categorical (nominal or ordinal) independent variable

Compare the mean blood pressure of a group of patients on a certain medication, with a predetermined value (normal blood pressure)

Independent two sample T-Test

Compares the mean of one distinct group to the mean of another distinct group to see if they are significantly different from each other.

It assumes that the variances of the two groups are equal (homogeneity of variance).

1 continuous dependent variable (performance score)

1 categorical independent variable (gender)

Compare mean performance scores between men and women

Paired Sample T-Test

Compares the means of two related groups.

It is used when the same subjects are measured twice (e.g. before and after treatment) or when there is a natural pairing (e.g. twin studies).

1 categorical independent variable (same people pre and post)

1 continuous dependent variable (anxiety score)

Does a meditation course decrease levels of anxiety

Analysis of Variance (ANOVA)

ANOVA is a statistical technique used to determine if there are significant differences between the means of three or more groups.

By comparing the variability within groups to the variability between groups, ANOVA assesses whether the observed differences in sample means are likely to occur by chance or if they reflect true differences in the populations.

Here is a summary of different types of ANOVA you can run and the conditions in which you would choose each test.

Test	Dependent Variable	Independent Variable	Number of Covariates	Example
One-way ANOVA	1 quantitative	1 categorical (≥3 groups)	None	To determine whether there are significant differences in average test scores among students from three different teaching methods (Method A, Method B, and Method C).
Two-way ANOVA	1 quantitative	≥ 1 categorical group	≥ 1	To investigate how different types of diets (Diet A, Diet B, and Diet C) and different exercise regimens (Exercise 1 and Exercise 2) affect weight loss in participants.
Repeated Measures ANOVA	1 quantitative (measured on ≥ 2 occasions or under different conditions)	≥ 1 categorical group	None	To assess the impact of a new therapy on anxiety levels by measuring the same participants' anxiety scores at three different time points (Before therapy, Immediately after therapy, and Three months post-therapy).

Correlation Analysis

The Pearson correlation coefficient is used to measure the strength and direction of the linear relationship between two variables.

Remember it does not necessarily signify causation!

If there is a significant correlation between the two variables, you then need to determine what direction the relationship is (positive or negative) the extent to which the two variables are related to each other (effect size or r-value) .

The direction of the relationship is indicated by the sign of the coefficient ( + indicates a positive relationship and a – indicates a negative relationship).

Positive correlation occurs when as one variable increases the other increases also.
Negative correlation is when one variable increases the other decreases.

The following table presents various $r$ r values in correlation analysis, along with their corresponding interpretations to help you understand the strength of relationships between variables.

R-Value	Interpretation
< 0.2	Very Slight
0.2 - 0.4	Low Correlation
0.4 - 0.7	Moderate Correlation
0.7 - 0.9	Strong Correlation
> 0.9	Very Strong Correlation

Non-Parametric Tests

In this section, you will find information on the non-parametric equivalents used in data analysis.

Common Parametric Tests and their Non-Parametric Equivalents
Parametric Technique	Non-Parametric Technique
Independent sample t-test	Mann-Whitney U test
Paired sample t-test	Wilcoxon Signed Rank Test
One way between groups ANOVA	Kruskal-Wallis Test

In this section, you will find information on some types of non-parametric tests used in data analysis.

Mann-Whitney U Test

You would conduct a Mann-Whitney U test to compare the differences between two independent groups on a continuous or ordinal outcome.
For example, a researcher might use the Mann-Whitney U test to compare the median recovery times between two different treatment groups where the recovery times are not normally distributed.
Wilcoxon Signed Rank Test

You would conduct a Wilcoxon Signed Rank Test when you want to compare the differences between two related groups or conditions on a continuous or ordinal outcome.
For example, a researcher might use the Wilcoxon Signed Rank Test to compare the median pain scores before and after a treatment intervention in the same group of patients.
Kruskal-Wallis Test

You would conduct a Kruskal-Wallis Test when you want to compare the median values of a continuous or ordinal outcome variable across three or more independent groups,
For example, you might use the Kruskal-Wallis Test to compare the median exam scores among students who studied using three different study methods.
Correlation Analysis
The most common non-parametric correlation coefficient is the Spearman rank correlation coefficient.
Remember correlation analysis does not necessarily signify causation!
If there is a significant correlation between the two variables, you then need to determine what direction the relationship is and the extent to which the two variables are related to each other.
The direction of the relationship is indicated by the sign of the coefficient ( + indicates a positive relationship and a – indicates a negative relationship).
- Positive correlation occurs when as one variable increases the other increases also.
- Negative correlation is when one variable increases the other decreases.
The strength of correlation indicates how closely the data points cluster around a straight line on a scatter plot. It is typically measured by the correlation coefficient, such as $\rho$ ρ.
- A correlation coefficient close to 1 or -1 indicates a strong correlation.
- A correlation coefficient close to 0 indicates a weak correlation.

Transforming Data

If your variables are not normally distributed, you may be able to mathematically transform the variables so that they are normally distributed.

There are different types of transformations and the choice depends on the distribution of the data.

Here are some common transformations and their effects on skewness:

Positive Skewness (Right Skewed):

Logarithmic Transformation: This reduces right skewness by compressing larger values more than smaller values.
Square Root Transformation: This reduces right skewness by compressing larger values more than smaller values.
Reciprocal Transformation: This reduces right skewness by attenuating larger values more than smaller values.

Negative Skewness (Left Skewed):

Exponential Transformation: This increases left skewness by stretching out smaller values more than larger values.
Square Transformation: This increases left skewness by stretching out smaller values more than larger values.
Cubic Transformation: The cubic transformation can increase or decrease skewness depending on the data, but it tends to increase left skewness.

These transformations can be applied to data to make them more symmetric and more likely to meet the assumptions of statistical tests or models.

However, the choice of transformation should be based on the characteristics of the data and the objectives of the analysis.

Experimentation and diagnostic tests are often necessary to determine the most appropriate transformation.